手書き数字認識
今回は前回に続きニューラルネットワークを扱います。
データはscikit-learnの手書き数字画像で、以下のような流れとなります。
- 64個の特徴量(8×8の画像データ)を持つデータセットを用意
- 学習用とテスト用に分割しtensor型に変換
- モデルにデータを学習させ、それを評価
- 精度が向上する(誤差が小さくなる)ことをグラフで確認
'''ライブラリの準備'''
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
'''データセットの準備'''
from sklearn import datasets
from sklearn.model_selection import train_test_split
digits_data = datasets.load_digits()
◆ライブラリとデータセットの準備
まずはライブラリとデータセット(手書き画像)を用意します。
この時点でdigits_dataのデータセットは、「画像ファイルの集まりではなく中身が数値で表現されている」という点に注意してください。
この画像データは8×8ピクセルの16階調のグレースケール画像を、薄い(0)〜濃い(16)の数値で表現されています。
◆データセットの表示
またデータセットが辞書型なのでdir()を使ってキーを確認することができますが、皆さんは特に確認なさらなくても大丈夫です。
ちなみにデータセットの中身はprint(digits_data)で確認でき、それぞれの要素の配列はshape()を使って確認できます。
※例えば、digits_dataの中の「data」というキーを確認したいときには、print(digits_data.data.shape)を実行すれば良いです。
'''データの表示'''
plt.figure(figsize=(10, 4))
for i in range(10):
ax = plt.subplot(2, 5, i+1)
plt.imshow(digits_data.data[i].reshape(8, 8), cmap="Greys_r")
plt.title(i)
ax.axis('off')
plt.show()
まずは表示する画像の数をn_imgという変数にセットします。
そして画像サイズをplt.figure(figsize=(横インチ, 縦インチ), dpi=解像度, facecolor=グラフの余白色, edgecolor=’k’)で指定します。
一度に複数画像を閲覧したかったので、plt.subplot(行の分割数, 列の分割数, 左上から何番目か)を使いました。
次にplt.imshowを使って、数値データから画像ファイルを表示します。
ここではreshapeを使って画像サイズを「64×1→8×8」に変換し、cmapで画像の色を指定しました。
※上のような解像度の低い0~9の数字の画像(8×8サイズ)が1797個含まれています。
'''学習データの準備'''
x_train, x_test, y_train, y_test = train_test_split(digits_data.data, digits_data.target, test_size=0.25, random_state=42)
'''tensor型へ変換'''
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train)
x_test = torch.FloatTensor(x_test)
y_test = torch.LongTensor(y_test)
'''モデルの定義'''
net = nn.Sequential(
nn.Linear(64, 32),
nn.ReLU(),
nn.Linear(32, 16),
nn.ReLU(),
nn.Linear(16, 10)
)
'''最適化手法の定義'''
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.01)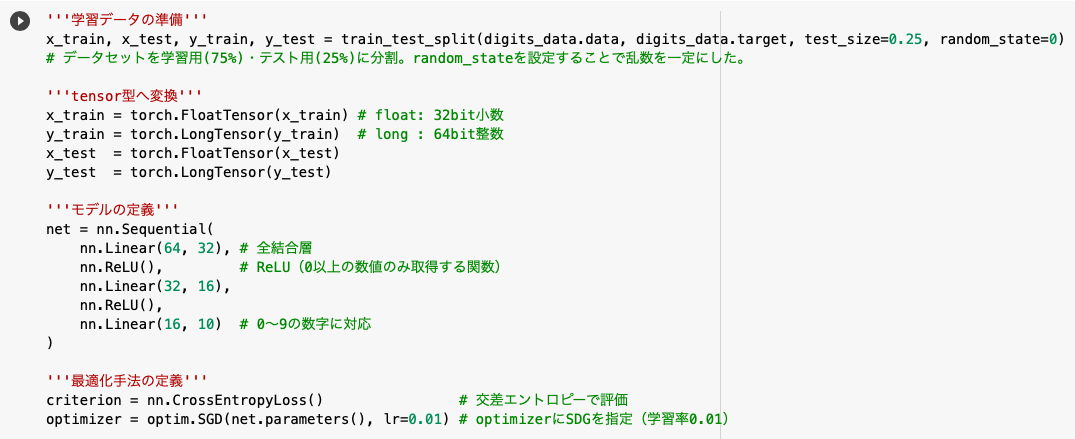
◆学習データの準備
まずは前回同様、train_test_spritでデータセットを(学習用とテスト用に)分割します。
その際にtest_sizeでテストデータの割合を決定し、random_stateで乱数を一定にしました。
※random_stateを設定することで、誰が実行しても同じ結果を得ることができます。再現性が求められる研究には必須の設定です。
◆モデルと最適化手法の定義
その後データをtensor型に変換し、nn.Sequential内でモデルを定義しました。
前回は以下の画像のようにnn.Moduleクラスを継承して、コンストラクタ(__init__)やfoward内で関数を記述しました。
しかしnn.Sequentialを使う場合は直接、全結合層(nn.Linear)や活性化関数(F.relu)を流れるように記述することができるのです。

モデルが定義できたら今度は最適化手法を定義します。
今回も交差エントロピー誤差(nn.CrossEntropyLoss)で評価し、optimizerにはSDGを採用しました。
'''損失(loss)を記録する空の配列を用意'''
record_loss_train = []
record_loss_test = []
'''学習'''
for i in range(1001):
optimizer.zero_grad()
x_train_net = net(x_train)
x_test_net = net(x_test)
loss_train = criterion(x_train_net, y_train)
loss_test = criterion(x_test_net, y_test)
record_loss_train.append(loss_train.item())
record_loss_test.append(loss_test.item())
loss_train.backward()
optimizer.step()
if i%100 == 0:
print("Epoch:", i, "Loss_Train:", loss_train.item(), "Loss_Test:", loss_test.item())
損失の推移を記録するために学習データ(train)とテストデータ(test)でそれぞれ空の配列を用意しました。
そしていつも通り、以下の処理をfor文で回すことで学習を進めます。
- optimizer.zero_grad()で勾配をクリア
- 特徴量を持ったデータをモデル(net)に学習させる(順伝播)
- 学習したデータと正解データの誤差を評価
- .backward()で各変数の勾配を求める(逆伝播)
- optimizer.step()でパラメータの更新
確認のためにprintで損失を出力しましたが、学習が進む(epochが増える)ごとに誤差が小さくなっていることが分かります。
※復習ですが、.item()を使うことでtensorの値のみを取得できます。
'''損失推移(record_loss)の可視化'''
plt.plot(range(len(record_loss_train)), record_loss_train, label="Train")
plt.plot(range(len(record_loss_test)), record_loss_test, label="Test")
plt.legend()
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.show()
'''正解率'''
accuracy = (net(x_test).argmax(1) == y_test).sum().item() / len(y_test)
print("正解率:", round(accuracy*100,1) , "%")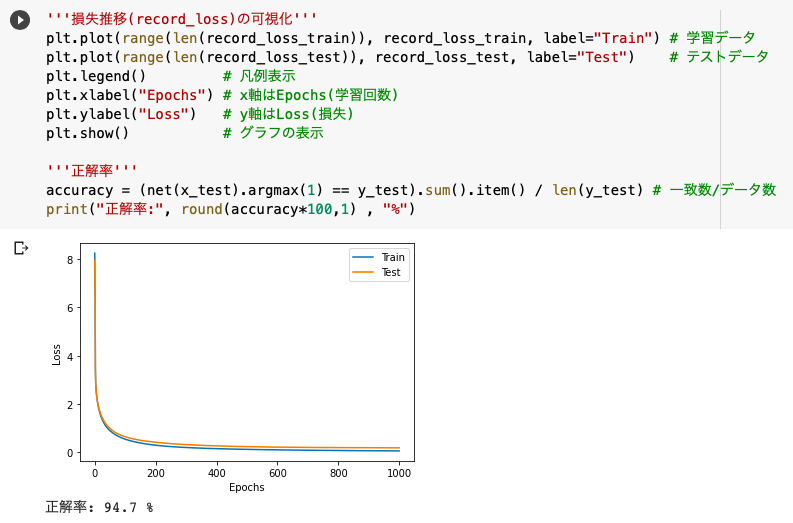
◆損失推移の可視化
先ほどfor文を回した際に記録した損失の推移(record_loss_train, record_loss_test)を可視化します。
ちなみにplt.plot(x, y)でx,y軸に座標を打つことができ、range(len(record_loss_train))は0~1001の範囲を表します。
※この0~1001の各インデックスに対応する結果(record_loss_train)を表示することで、上の曲線が実現します。
◆正解率
次に正解率(全要素の中の一致数/全要素数)の計算について解説します。
一致数は「net(x_test):学習済データ」と「y_test:正解データ」を比較するのですが、これらはtensor型なので.sum().item()の処理を加える必要があります。
中身はこんな感じです。
net(x_test)は各画像において「0~9の数値だと認識された確率」を示しており、今回は*argmax(詳しくは後述)でその確率が最大となるインデックス、すなわち「最も確率が高いと認識された数」を取得しています。
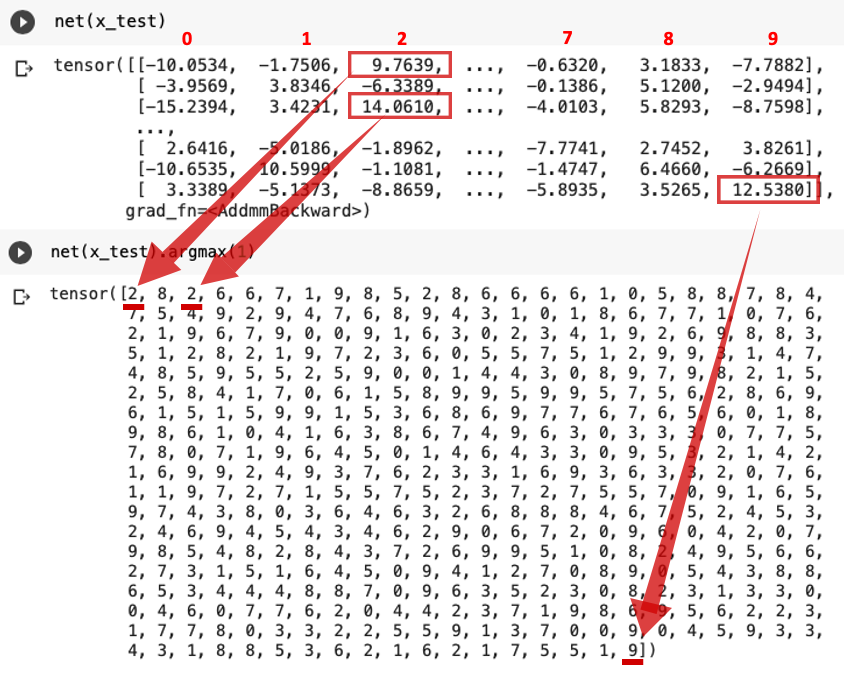
◆argmax
argmax()は「最大値をとるインデックスを返す」という役割を持ち、引数に0/1をセットすることで列方向/行方向を指定します。
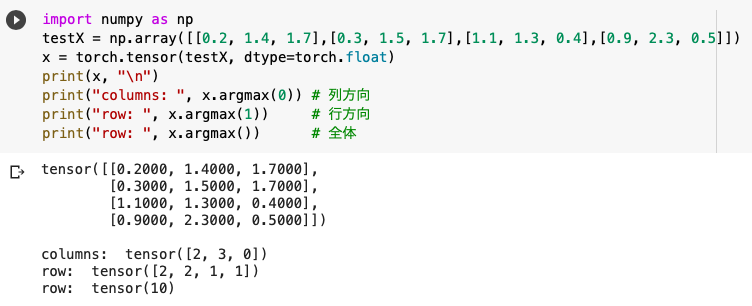
'''実験'''
img_id = 1234
x_pred = digits_data.data[img_id]
image = x_pred.reshape(8, 8)
plt.imshow(image, cmap="Greys_r")
plt.axis('off')
plt.show()
y_pred = net(torch.FloatTensor(x_pred))
print("正解:", digits_data.target[img_id], "予測結果:", y_pred.argmax().item())
実験では各自で「img_id」の値を変更することで、様々な手書き数字を識別させることができます。
(正解率が90%を超えているのでほとんど正しい結果が返ってくると思いますが)
さて、ここまでPyTorchを使った予測も少しできるようになったので、今度はその精度の高め方について見ていきたいと思います。
モデルの精度を高める
モデルの精度を高める前に、気をつけなければならないのが「重みの初期化」です。
機械学習でモデルを回す度に重みが最適化されるので、それを初期化する必要があります。
※以下のコードを「学習」の前に挿入してください。
'''重みの初期化(前の学習を初期化)'''
def init_weights(m):
if type(m) == nn.Linear:
torch.nn.init.xavier_uniform(m.weight)
m.bias.data.fill_(0.01)
net.apply(init_weights)
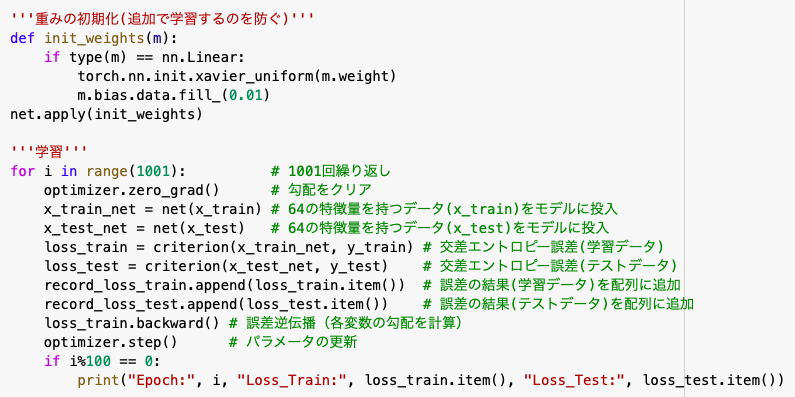
準備が整いましたら各パラメータの値を調整し、結果をみていきます。
◆学習率
※最適化手法の定義の「optimizer = optim.SGD(net.parameters(), lr=0.01)」
・lr=0.001のとき:86.5%
・lr=0.005のとき:95.3%
・lr=0.01のとき:94.7%
・lr=0.05のとき:93.8%
・lr=0.1のとき:96.9%
◆テストデータの割合
※学習データ準備の「x_train, x_test, y_train, y_test = train_test_split(digits_data.data, digits_data.target, test_size=0.25, random_state=0)」
・test_size=0.10のとき:97.2%
・test_size=0.18のとき:96.0%
・test_size=0.25のとき:94.7%
・test_size=0.32のとき:95.7%
・test_size=0.40のとき:95.4%
◆エポック数(処理を繰り返す回数)
※学習の「for i in range(1001)」
・epoch=301のとき:89.3%
・epoch=501のとき:93.1%
・epoch=1001のとき:94.7%
・epoch=1501のとき:96.0%
・epoch=2001のとき:97.1%
◆中間層のノード数
※モデルの定義の「net = nn.Sequential()の中のnn.Linearの64→32→16→10」
・64→16→10→10のとき:96.0%
・64→16→16→10のとき:94.0%
・64→32→16→10のとき:94.7%
・64→64→64→10のとき:96.2%
・64→128→64→10のとき:97.6%
◆中間層の数
※モデルの定義の「net = nn.Sequential()の中のnn.Linearの64→32→16→10」
・64→16→10のとき:96.2%
・64→32→16→10のとき:94.7%
・64→32→16→16→10のとき:95.6%
・64→32→32→16→16→10のとき:96.4%
・64→64→32→32→16→16→10のとき:93.3%
◆損失関数
※最適化手法の定義の「optimizer = optim.SGD(net.parameters(), lr=0.01)の中のSGD」
・SGD:94.7%
・Adam:96.9%
・Adam-AMSGrad:96.4%
・Adagrad:96.7%
・RSMprop:94.4%
※AMSGradは勾配のノルムの二乗から計算される値の最大値で勾配を抑えることでAdamの収束性を改善したものである。Adamの引数に「amsgrad=True」を入れて使い、今回の例では「Adam(net.parameters(), lr=0.01, amsgrad=True)」とする。
参考文献
scikit-learnで手書き文字認識
手書き数字がずのデータセットを機械学習で多クラス分類
matplotlibで出力される画像サイズを変更する
matplotlibのグラフを入れ子に!subplotを使おう
ニューラルネットワークによる手書き数字の認識
CNNをPyTorchのSequentialを使って実装する
PyTorch reference
pytorch for pythonにおける損失関数
機械学習における損失関数の役割や種類
Optimizerに関する備忘録









この記事へのコメントはありません。